AI Reasoning on IMO(International Mathematical Olympiad)
Summary
The article explores AI's progress in solving International Mathematical Olympiad (IMO) problems, focusing on DeepMind's AlphaGeometry and AlphaProof, which achieved silver-medal performance in 2024. It discusses AI's potential to automate theorem proving, the history of theorem provers, and challenges like spatial reasoning and meta-planning, particularly with IMO's Problem 6.
Introduction
The International Mathematical Olympiad (IMO) represents the highest level of mathematical competition for high schoolers , challenging exceptional students with problems requiring profound creativity and analytical precision. As of July 20, 2025, artificial intelligence systems are making significant strides toward IMO mastery, with gold medal performance considered achievable by solving 5 out of 6 problems, though a perfect score remains out of reach. This can be contrasted with much more advanced problems from FrontierMath, Humanity's Last Exam.
Why Mathematicians want to automate Mathematics
Mathematicians generally want automated theorem provers to rigorously verify complex proofs and eliminate human error, especially in long or intricate arguments. They also use them to accelerate formalization, explore conjectures, and offload routine steps, allowing more focus on creative insights. IMO Mathematics tends to be very different to Formal Mathematics, Gowers due to the universality of concepts they are allowed to use.
History of Theorem Provers
- 1950s–60s: Early systems like Logic Theorist and Robinson’s resolution method laid foundations for automated reasoning.
- 1970s–80s: Interactive theorem provers (e.g., LCF, Coq) emerged, enabling formal verification with human guidance.
- 1990s–2000s: Used in industry and academia to verify hardware and major theorems like the Four Color and Kepler Conjectures.
- 2010s–2020s: AI-enhanced provers and proof engineering gain traction, aiming to scale and accelerate formalized mathematics.
Tool Use
Mathematical formalism and AI tooling are increasingly intersecting, as seen in Talia Ringer's work on proof engineering and mechanized reasoning, highlighting how AI can support long-form formal verification tasks and collaborative theorem proving. AI models can be trained on theorem provers(such as Lean 4 ), as noted most base models tend to be accompanied by provers, such as Kimi K2 , Mistral
The Geometry Breakthrough
AlphaGeometry
In January 2024, DeepMind's AlphaGeometry, a neuro-symbolic AI, solved 25 of 30 IMO geometry problems, matching the average human gold medalist's performance DeepMind, 2024. Unlike prior methods like Wu's, which solved only 10 problems, AlphaGeometry combined a neural language model for intuitive predictions with a symbolic deduction engine for rigorous verification Chou, 1985. This hybrid approach mirrors human cognition's blend of intuition and logic. AlphaGeometry's success stemmed from generating 100 million synthetic geometry theorems, enabling training without human demonstrations. If the symbolic engine failed, the neural model added auxiliary points, iterating until a proof was found Trinh et al., 2024 Vaswani et al., 2017.
AlphaProof
AlphaProof's training optimized a reward function where scores proof steps, and discounts future rewards Sutton & Barto, 2018. Market sentiment on Manifold Markets, with a 66% probability of an AI gold medal by 2025, reflects optimism, driven by these results and expert endorsements from superforecasters.
The 2024- IMO Alpha Generation Performance
AlphaGeometry 2 and AlphaProof achieved a silver-medal score of 28/42 at IMO 2024, solving four of six problems DeepMind, 2024. AlphaGeometry 2, trained on tenfold more synthetic data, solved 83% of historical IMO geometry problems (2000–2024), up from 53%, tackling Problem 4 in 19 seconds by constructing point E to prove Chervonyi et al., 2025. AlphaProof, using reinforcement learning and the Lean language, solved two algebra problems and one number theory problem, including the hardest, solved by only five humans Li et al., 2022.
The Challenge of Solving Problem 6
This can be considered The Problem 6 Challenge , it is a kind of problem that would require Move 37-style discovery.
AlphaGo vs. Lee Sedol [Move 37]
Move 37 involved placing a stone on the 5th line, a position rarely seen in professional Go play, particularly in high-stakes games. It was initially perceived as a mistake or an inefficient move by human experts.
Spatial Reasoning and Meta-Planning
Despite these advances, AI struggles with spatial reasoning and meta-planning, critical for combinatorial problems. IMO 2024's Problem 6, solved by one human, exposed these limitations, as AlphaProof and AlphaGeometry 2 failed both combinatorics tasks DeepMind, 2024. Translating problems into formal languages like Lean remains a bottleneck, with manual intervention required. Additionally, AlphaGeometry 2 cannot handle problems with variable points or nonlinear equations, limiting its coverage to 88% of IMO geometry problems Chervonyi et al., 2025.
Integrating diverse mathematical traditions, such as Soviet or Indian geometric techniques, could enhance AI's flexibility, a hypothesis aligned with DeepMind's goal of generalizable reasoning Hooker, 2021.
Hyperpolation
Toby Ord introduced hyperpolation as the task of predicting or generalising beyond the subspace (or manifold) on which existing data lie—unlike interpolation (within) or extrapolation (along). Ord positions hyperpolation as a form of creativity in learning systems: estimating function values at points lying outside known data subspaces. Current AI systems struggle at it, and suggests this limitation is at the heart of their inability to exhibit fundamental creativity Humans tend to be good at superspace extrapolation
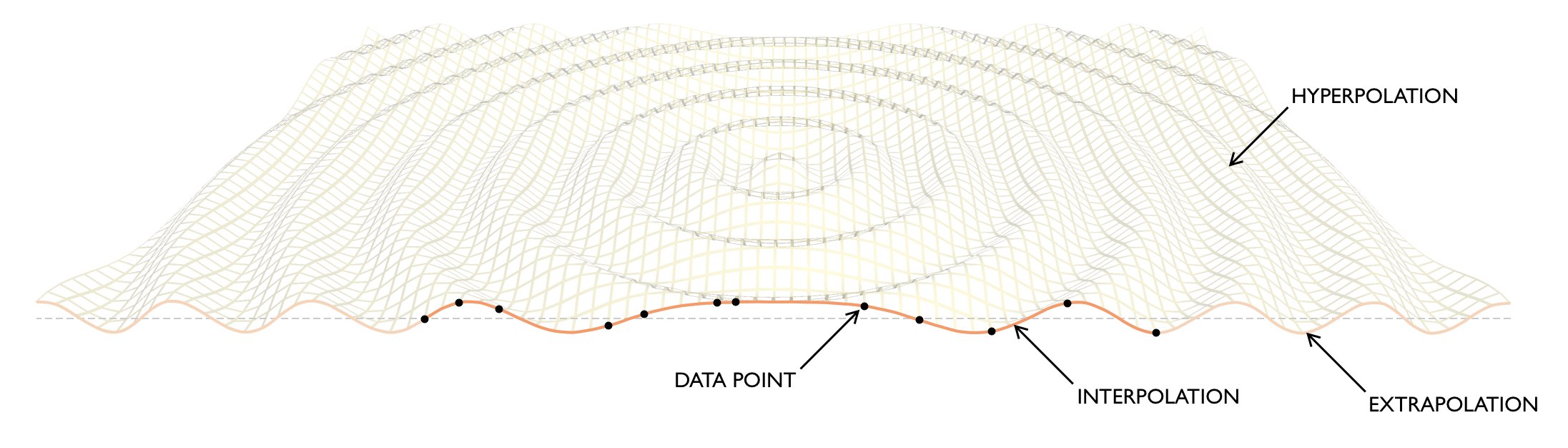
Figure 2: Hyperpolation illustrated
- Interpolation asks what lies between the examples we’ve already seen.
- Extrapolation asks what lies beyond them.
- Hyperpolation asks what lies in directions that can’t be defined in terms of the existing examples.
This phenomenon suggests that as model scale increases, LLMs can generalize to solve novel mathematical problems that require complex reasoning chains not explicitly present in training data.
IMO 2025: Tim Gowers' Analysis
Together with Sir Timothy Gowers, at the Human-Style Automated Theorem Prover Project we are aiming to understand in detail how humans find proofs, and then to use that understanding to program computers to find proofs in the same way. Many of the winners of the Fields Medal, one of the highest honors for mathematicians, have represented their country at the IMO, showcasing his approach to mathematical reasoning. Prof Gowers who won IMO Gold 1981 with a perfect score – 100%, known for his contributions to combinatorics and functional analysis, demonstrated expert problem-solving techniques without computational assistance.
Model Performance Comparison
The table below shows the performance of various AI models on the IMO 2025 competition, along with their overall accuracy and cost metrics:
| Model | Acc | Cost | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|
| gemini-2.5-pro | 31.55% | $431.97 | 14% | 0% | 71% | 46% | 57% | 0% |
| o3 (high) | 16.67% | $223.33 | 0% | 0% | 7% | 36% | 57% | 0% |
| o4-mini (high) | 14.29% | $103.34 | 16% | 0% | 5% | 46% | 18% | 0% |
| Grok 4 | 11.90% | $527.85 | 13% | 4% | 18% | 13% | 25% | 0% |
| DeepSeek-R1-0528 | 6.85% | $59.50 | 4% | 0% | 5% | 0% | 32% | 0% |
Are models any good at homeworks?
Recent work by Thomas Kwa et al. (2025) introduces the "50% task-completion time horizon" to measure how long AI agents can perform tasks before their success rate drops to 50%, showing top models like Claude 3.7 Sonnet reaching ~59 minutes on benchmark suites.
- Kwa shows that 80% task success occurs at around 1/3 of the half-life, 99% at 1/70th, and so on, aligning well with observed data.
- Terence Tao, Tao, Mathstodon notes that we should consider the context this exponential decay model allows principled comparisons across agents.
- Toby Ord (2025) comments that a half-life model concept in which AI success decays exponentially with task duration due to a constant failure hazard across subtasks; this explains empirical data and provides a benchmark-agnostic, interpretable metric.
"One gives the students several days to complete each question, rather than four and half hours for three questions. To stretch the metaphor somewhat, consider a sci-fi scenario in the student is still only given four and a half hours, but the team leader places the students in some sort of expensive and energy-intensive time acceleration machine in which months or even years of time pass for the students during this period." – Terence Tao
Together, these works suggest that AI’s ability to reliably complete long-horizon tasks is increasing rapidly, and the "half-life" concept offers a unified way to track this trend.
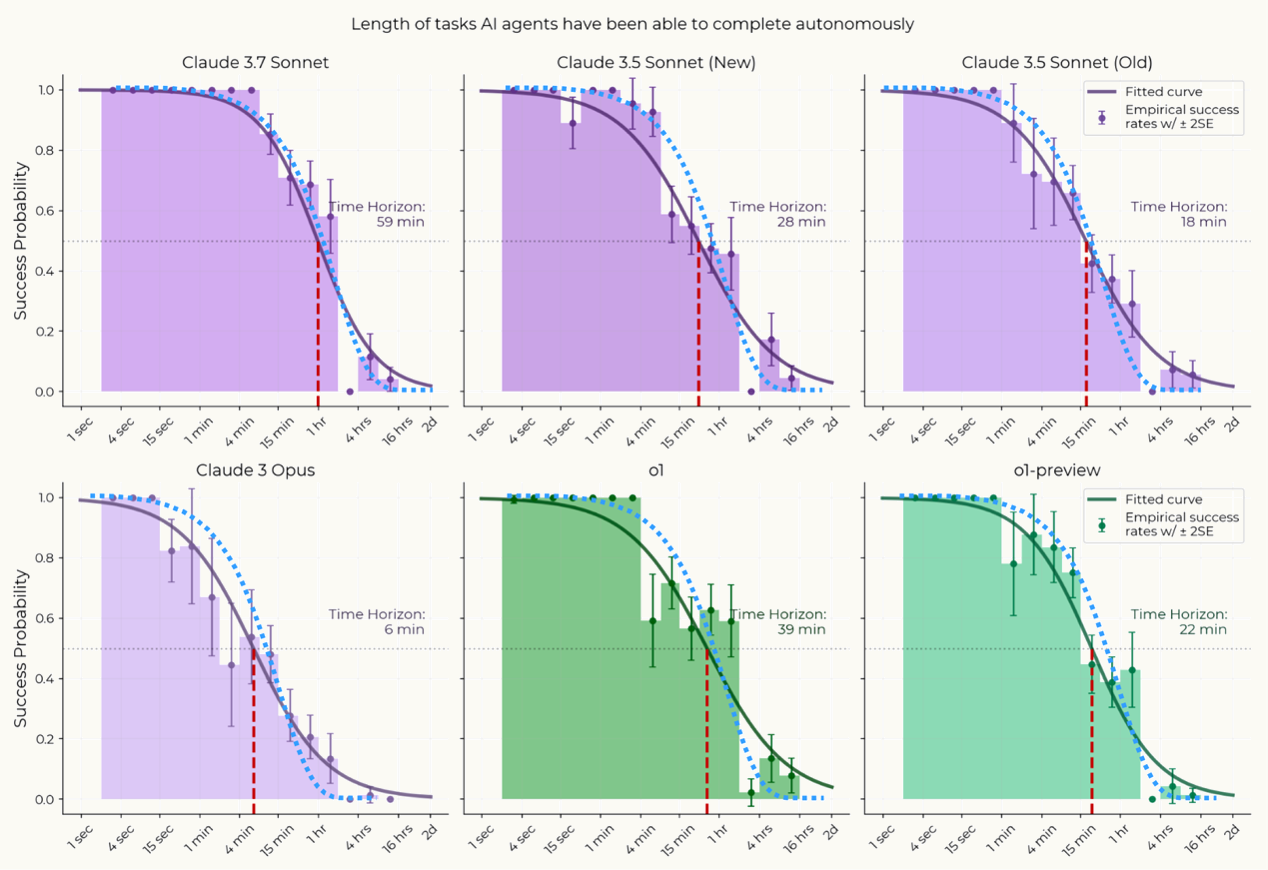
Figure 0: Thomas Kwa shows that 80% task success occurs at around 1/3 of the half-life, 99% at 1/70th, and so on.
Together, these works suggest that AI's ability to reliably complete long-horizon tasks is increasing rapidly, and the "half-life" concept offers a unified way to track this trend.
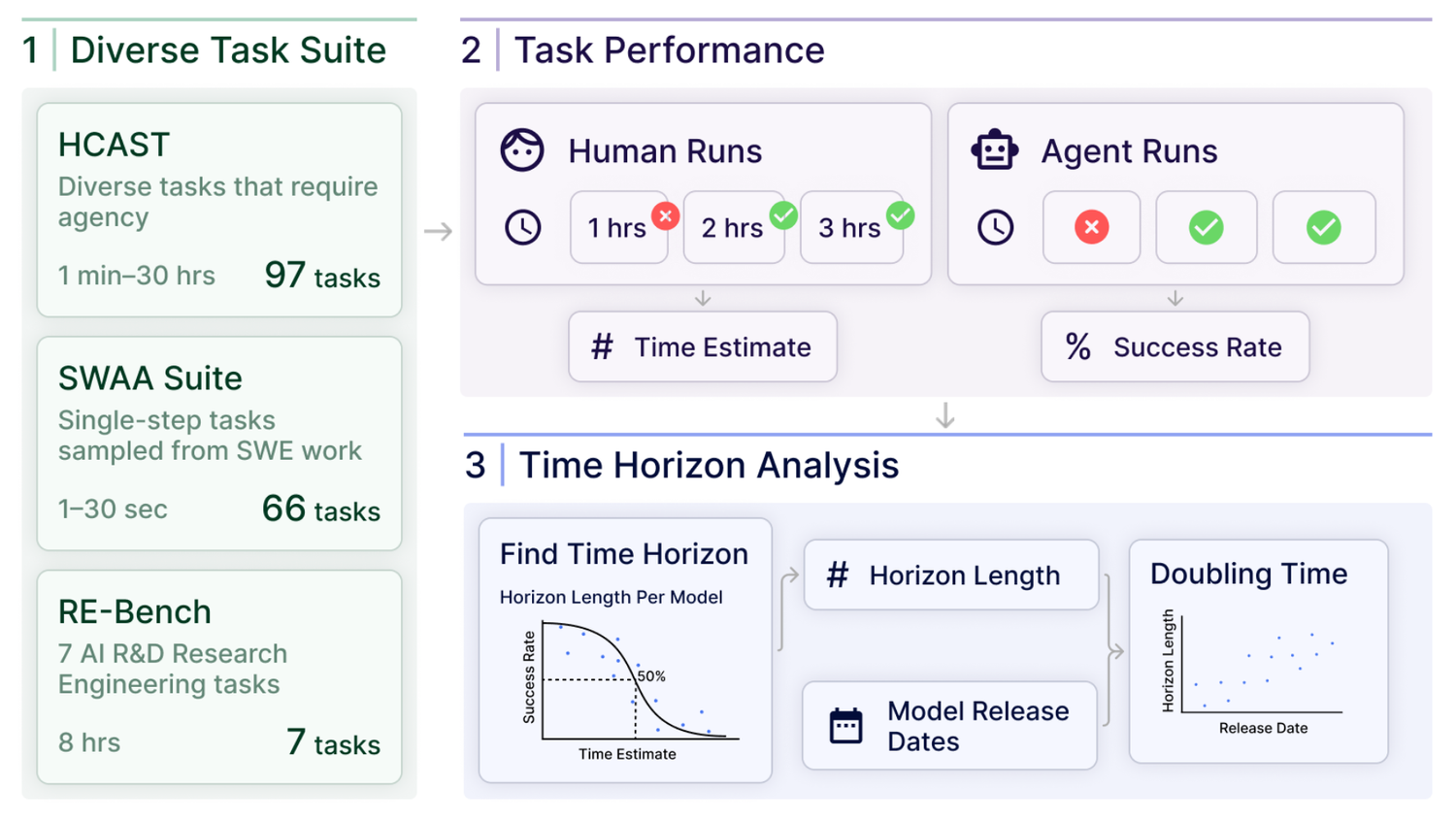
Figure 1: The models ability to perform a task drops off as its duration increases, so they use the AI agent's performance on tasks of different lengths to estimate the task-length at which the model would have a 50% success rate.
Problem 1. A line in the plane is called sunny if it is not parallel to any of the x-axis, the y-axis, and the line . Let be a given integer. Determine all nonnegative integers k such that there exist n distinct lines in the plane satisfying both of the following:
- for all positive integers a and b with , the point is on at least one of the lines; and
- exactly k of the n lines are sunny.
My Attempt for a Proof Sketch
This is a human-inspired approach in which we would set the predicates for the first problem.
My Proof Sketch attempt For n = 3, we need to cover:
Let's consider what happens with non-sunny lines (those parallel to the x-axis, y-axis, or the line ):
- A horizontal line covers points etc.
- A vertical line covers points etc.
- A line covers points where
I'll show that is always possible, and no other values of k are valid.
Case n=3: Points to Cover
Case n=4: Points to Cover
What's Next for AI in Mathematics?
The IMO serves as a benchmark for AI reasoning, akin to chess for earlier computational challenges. AlphaGeometry's human-readable proofs, using classical geometry, avoid brute-force algebra, offering "verifiable and clean" solutions, as noted by Evan Chen DeepMind, 2024. DeepMind's experiments with natural language reasoning, built on Gemini, aim to eliminate manual translations, promising broader applicability Chervonyi et al., 2025. A 66% market probability suggests AI may achieve an IMO gold medal by 2025, I argue spatial reasoning remains a frontier bottleneck. The $5M AI Mathematical Olympiad Prize incentivizes progress, but DeepMind's closed-source systems are ineligible Gerko, 2024.
Conclusion: A Collaborative Future
On July 20, 2025, AI's progress in the IMO underscores a shift toward machine-human collaboration in mathematics. AlphaGeometry and AlphaProof are not just solving problems—they're redefining reasoning and discovery. As hardware and algorithms evolve, addressing spatial reasoning and meta-planning could unlock an IMO gold medal by 2026, supporting a future where AI augments mathematical exploration. Will 2025 mark the turning point? The journey continues.
References
- Vaswani, A., et al. (2017). Attention is All You Need. arXiv:1706.03762.
- Sutton, R. S., & Barto, A. G. (2018). Reinforcement Learning: An Introduction. MIT Press.
- Li, Y., et al. (2022). Competition-Level Code Generation with AlphaCode. arXiv:2112.00114.
- DeepMind. (2024). AlphaGeometry: An Olympiad-Level AI System for Geometry.
- DeepMind. (2024). AI Solves IMO Problems at Silver Medal Level.
- Trinh, T. H., et al. (2024). AlphaGeometry: Solving Olympiad Geometry without Human Demonstrations. arXiv:2401.09319.
- Chervonyi, Y., et al. (2025). Gold-Medalist Performance in Solving Olympiad Geometry with AlphaGeometry2. arXiv:2502.03544.
- Hooker, S. (2021). The Hardware Lottery. arXiv:2009.06489.
- Thomas Kwa et al., Measuring AI Ability to Complete Long Tasks, arXiv:2503.14499 [cs.AI], 2025.
- Toby Ord, The Lindy Effect. arXiv:2308.09045 [physics.soc-ph], 2023.